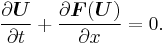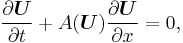Roe solver

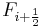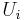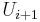The Roe approximate Riemann solver, devised by Phil Roe, is an approximate Riemann solver based around the Godunov scheme and involves finding an estimate for the intercell numerical flux or Godunov flux $F_{i %2B \frac{1}{2}}$ at the interface between two computational cells $U_{i}$ and $U_{i%2B1}$ , on some discretised space-time computational domain.

1 The Roe Scheme
2 References
3 Further reading

The Roe Scheme

Quasi-linear Hyperbolic system

A non-linear system of hyperbolic partial differential equations representing a set of conservation laws in one spatial dimension can be written in the form

$\frac{\partial \boldsymbol{U}}{\partial t} %2B \frac{\partial \boldsymbol{F}(\boldsymbol{U})}{\partial x} = 0.$

Applying the chain rule the second term we get the quasi-linear hyperbolic system

$\frac{\partial \boldsymbol{U}}{\partial t} %2B A(\boldsymbol{U})\frac{\partial \boldsymbol{U}}{\partial x} = 0,$

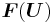where $A$ is the jacobian matrix of the flux vector $\boldsymbol{F}(\boldsymbol{U})$ .

The Roe Matrix

The Roe method consists of finding a matrix 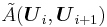$\tilde{A}(\boldsymbol{U}_i,\boldsymbol{U}_{i%2B1})$ that is assumed constant between two cells. The Riemann problem can then be solved as a truly linear hyperbolic system at each cell interface. The Roe matrix must obey the following conditions:

Diagonalizable with real eigenvalues Ensures that the new linear system is truly hyperbolic.
Consistency with the exact jacobian When 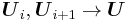$\boldsymbol{U}_i,\boldsymbol{U}_{i%2B1} \rightarrow \boldsymbol{U}$ we demand that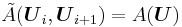 $\tilde{A}(\boldsymbol{U}_i,\boldsymbol{U}_{i%2B1}) = A(\boldsymbol{U})$
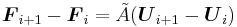
Conserving $\boldsymbol{F}_{i%2B1}-\boldsymbol{F}_{i} = \tilde{A}(\boldsymbol{U}_{i%2B1}-\boldsymbol{U}_{i})$

Phil Roe introduced a method of parameter vectors^[1] to find such a matrix for some systems of conservation laws.

The Intercell Flux

Once the Roe matrix corresponding to the interface between two cells is found, the intercell flux is given by solving the quasi-linear system as a truly linear system.

References

^ P. L. Roe, Approximate riemann solvers, parameter vectors and difference schemes, Journal of Computational Physics, 43, 357-372, (1981)